

Plug the value into the original equation to get the value.
Standard form quadratic equation plus#
So this is going to be negative 20 plus 15, which is equal to negative 5. The formula for finding the x-value of the vertex of a quadratic equation is. Note that the quadratic formula actually has many real-world applications, such as calculating areas, projectile trajectories, and speed, among others. When x equals 2, y is going to be equal to 5 times 2 squared minus 20 times 2 plus 15, which is equal to- let's see, this is equal to 2 squared is 4. The numerals a, b, and c are coefficients of the equation, and they represent known numbers. where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. If a parabola is given in another form it must be converted to Standard Form. In algebra, a quadratic equation is any polynomial equation of the second degree with the following form: ax 2 + bx + c 0. The quadratic formula only can be used to find the zeros of a parabola in Standard Form. The examples given in the previous lesson were all given in Standard Form. This is demonstrated by the graph provided below. Standard Form of a Parabola can be very useful for analyzing parabolas. Furthermore, the quadratic formula also provides the axis of symmetry of the parabola. The x values found through the quadratic formula are roots of the quadratic equation that represent the x values where any parabola crosses the x-axis. Recall that the ± exists as a function of computing a square root, making both positive and negative roots solutions of the quadratic equation. Below is the quadratic formula, as well as its derivation.įrom this point, it is possible to complete the square using the relationship that:Ĭontinuing the derivation using this relationship: Only the use of the quadratic formula, as well as the basics of completing the square, will be discussed here (since the derivation of the formula involves completing the square). A quadratic equation can be solved in multiple ways, including factoring, using the quadratic formula, completing the square, or graphing.

For example, a cannot be 0, or the equation would be linear rather than quadratic.
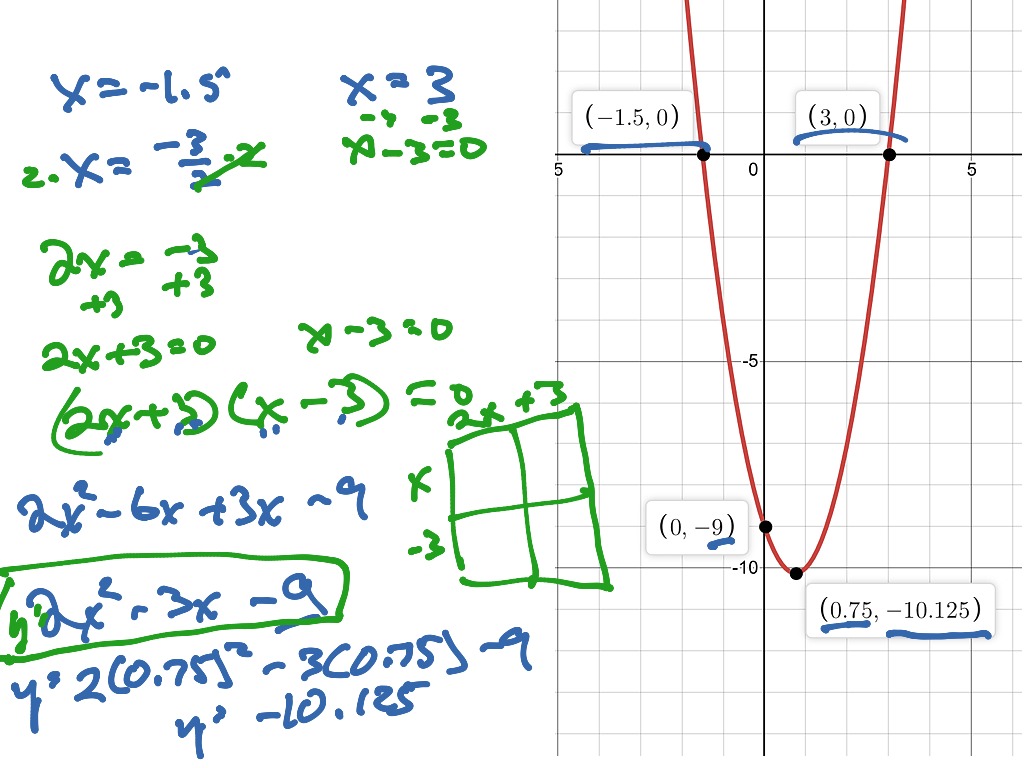
If a is positive, the graph opens upward, and if a is negative. Where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. The quadratic function f(x) a(x - h)2 + k, a not equal to zero, is said to be in standard form. In algebra, a quadratic equation is any polynomial equation of the second degree with the following form: Fractional values such as 3/4 can be used.


 0 kommentar(er)
0 kommentar(er)
